Hi,
I’m looking for a diagonal grid drawing algorithm. I know, it should be only a double loop method like for a normal grid. The drawing should take place in an assigned rectangle (probably you will have to use Graphics.Clip) So the width and height for the pattern fill are given. How can something like this be realized easily?
If you have a defined rectangle, just use g.DrawLine to draw your diagonals within that area. Assuming you want symmetrical diamond shapes (diagonal squares), you would draw 45 degree diagonal lines, which means equal width and height points for the line. So, for a given spacing, you start at the “small” corner (lower right for the / lines and lower left for the \ lines) and set your points (x and y) to a multiple of the spacing until you reach the limit of the rectangle (width or height if it’s not square).
If you want other diamond shapes (“taller” or “wider”), then you’ll need to do some right-angle triangle calculations to determine the start and stop points for DrawLine.
Thank you @jmadren and how could that look in code? 
Another idea is if you have a fixed “pattern” you want to use in all scenarios, just create an image containing the pattern that’s as large as the maximum drawing area you anticipate, then use Graphics.Clip on that as you suggested. You could even create this image at app startup using the method I laid out before. Will require testing to determine which way is faster.
Ok, took a little while to figure it all out, but the following placed in the Paint event will give you 45 degree diagonals both ways that fill the defined area:
Var spacing, ax1, ay1, ax2, ay2, x1, x2, y1, y2 As Integer
spacing = 10
//define area to draw, starting at ax1,ay1 (upper left) to ax2,ay2 (lower right)
ax1 = 25
ay1 = 25
ax2 = ax1 + 87 //area is 87 wide
ay2 = ay1 + 45 //area is 45 tall
//draw / lines from x1,y1 (lower-left) to x2,y2 (upper-right), starting from upper-left corner of area
x1 = ax1
y1 = ay1 + spacing
x2 = ax1 + spacing
y2 = ay1
While x1 < ax2 Or y1 < ay2 Or x2 < ax2 Or y2 < ay2
g.DrawLine(Min(x1, ax2), Min(y1, ay2), Min(x2, ax2), Min(y2, ay2))
y1 = y1 + spacing
If y1 > ay2 Then
If x1 = ax1 Then x1 = ax1 + (y1 - ay2) Else x1 = x1 + spacing
End If
x2 = x2 + spacing
If x2 > ax2 Then
If y2 = ay1 Then y2 = ay1 + (x2 - ax2) Else y2 = y2 + spacing
End If
Wend
//draw \ lines from x1,y1 (upper-left) to x2,y2 (lower-right), starting from upper-right corner of area
x1 = ax1 + (((ax2 - ax1) \ spacing) * spacing) //highest multiple of spacing that is within width
y1 = ay1
x2 = x1 + spacing
y2 = ay1 + (x2 - ax2)
While x1 > ax1 Or y1 < ay2 Or x2 > ax1 Or y2 < ay2
g.DrawLine(Max(x1, ax1), Min(y1, ay2), Min(x2, ax2), Min(y2, ay2))
x1 = x1 - spacing
If x1 < ax1 Then y1 = y1 + spacing
y2 = y2 + spacing
If y2 > ay2 Then
If x2 > ax2 Then x2 = ax2 - (y2 - ay2) Else x2 = x2 - spacing
End If
Wend
If you want angles other than 45 degrees, it will take some additional calculating and logic.
1 Like
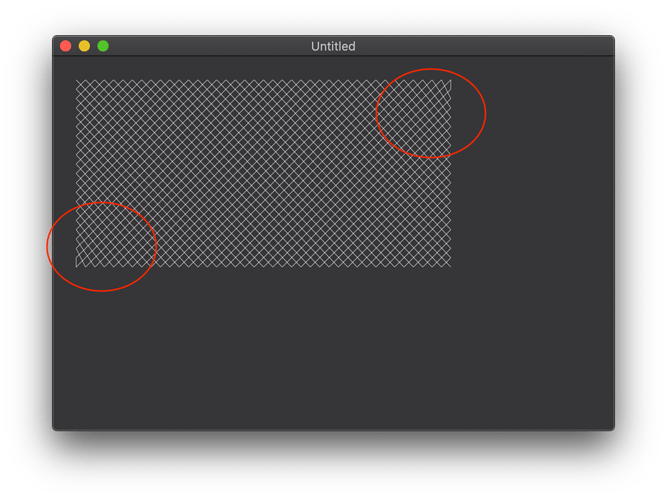
Sorry for the late reply and thanks for your suggestion. I noticed from the result of your algorithm that the grid looks “weird” in two places.
What are the dimensions for this area? Looks like it’s a case of the two x values being equal, so probably need to add an exclusion or exception in that case.
It is exactly the code that you have provided. I haven’t changed anything, just increased the width and height a bit. But even with your code, something seems to be wrong in those areas. The diamonds seem a little larger than the ones above it, do you see that?
maybe something like this ?
this is in the paint event of a canvas placed on window1
the window has a textfield for angle and step size
If txtAngle.Text.Trim = "" Or txtStep.Text.Trim = "" Then
Return
End If
Const pi = 3.1415926535897932384626433
Dim angle As Double = Val(txtAngle.Text)
Dim stepSize As Integer = Val(txtStep.Text)
If angle = 0 Or stepsize = 0 Then
Return
End If
Dim angleInRadians As Double = (angle * pi) / 180
Dim lineLength As Integer = g.width * 3
g.forecolor = &cFFFFFF
Dim x1 As Double
Dim x2 As Double
Dim y1 As Double
Dim y2 As Double
// make sure we start drawing down & right far enough off the LEFT edge that the X2 starts <= 0
Dim x1Start As Double
x2 = x1Start + lineLength * Cos(angleInRadians)
While x2 > 0
x1Start = x1Start - stepSize
x2 = x1Start + lineLength * Cos(angleInRadians)
Wend
// draw down and right from the top edge
x1 = x1Start
y1 = 0
Do
// now compute x2, y2
x2 = x1 + lineLength * Cos(angleInRadians)
y2 = y1 + lineLength * Sin(angleInRadians)
g.DrawLine x1, y1, x2, y2
x1 = x1 + stepSize
Loop Until x1 > g.width
// draw down and left from the top edge
x1 = 0
y1 = 0
Do
// now compute x2, y2
x2 = x1 - lineLength * Cos(angleInRadians)
y2 = y1 + lineLength * Sin(angleInRadians)
g.DrawLine x1, y1, x2, y2
x1 = x1 + stepSize
Loop Until x2 > g.width
1 Like
Great Norman and James, thanks. Now it looks good. What have you modified Norman?
I didnt modify anything
I wrote that from scratch 
it draws down & right in one loop starting far enogh left that every line is drawn
If you start the first loop at x=0 it misses the whole lower left corner
so we have to figure out how far left to move to draw so that we fill that area too
then down & left in another
and does so enough that the lower x eventually exceeds the width of the graphics area
the math may not be all perfect if the angle isnt 45 degrees
it was just my approach to the problem
1 Like
How did you arrive at the multiplication factor of 3?
experiments
BUT much like I computed x1Start you could actually computer the line length required
dim lineLength as integer = 10
// lets figure out the right line length
y2 = y1 + lineLength * Sin(angleInRadians)
While y2 < g.height
lineLength = lineLength + stepSize
y2 = y1 + lineLength * Sin(angleInRadians)
Wend
and this will compute a line length that will, when drawn at the angle, go from y1 to the height of the graphics area
note linelength needs to start at some non-zero value or you get an infinite loop 
EDIT : I have replaced the zip file with one including this tweak
1 Like