Breadth First vs Depth first searches

General Programming
1

Since someone asked the question I’ll answer

Usually depth first and breadth first search apply to hierarchically organized data. This might be described as a “tree”.
Note that we dont have to actually be “searching”. We can use the traversal as a search or a way to print out the dat a in specific orders etc.

A directory hierarchy would be a great example.
In there you have directories with files and possibly other directories.

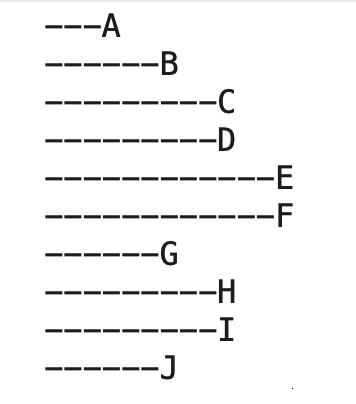
Lets assume, for this discussion, you have a tree like

 a
	b
		c
		d
			e
			f
	g
		h
		i
	j

a is the “top” and everything is contained by a
Thats really not a requirement but it make is easier to talk about the algorithms

In a depth first traversal you try to go down the tree as deeply as possible before you go across/so if we were to traverse our sample depth first using the following mechanism (stated in pseudo code)

ProcessNode
      if node has children then
             for all children ProcessNode 
     end if
     print node value

the results would be

             e
             f
             d
             b
             h
             i
             g
             j
             a

The point is the algorithm dives in as deeply as possible BEFORE doing anything with the current node, hence “depth first”

Breadth first is quite different. Breadth first process entire “layers” of the hierarchy before moving deeper into the hierarchy. As such it’s algorithm is quite different and its actually easier to write as a non-recursive algorithm (depth first can be written not recursively as well using a similar technique)

ProcessNode( node )
        create a queue 
        add the node passed to the queue
        while the queue is not empty
             set thisnode to the node at the front of the queue
             process thisnode
             add all children of thisnode to the end of the queue
             remove thisnode from the front of the queue
        wend

The results of this kind of traversal are

             a
             b
             g
             j
             c
             d
             h
             i
             e
             f

There are other kinds of traversals as well that are suited to other kinds of data structures

Heres a sample in Xojo

1 Like
2

Ok… I am trying to make sense of this and failing… :frowning:

I have an array of structures… the two important fields in the structure are PARENT and CHILD, a node with a blank parent is the root of the tree (there will be and must be only ONE)

so in Norms first post

would be
“”,A
A,B
B,C
B,D
D,E
D,F
A,G
G,H
G,I
A,J

These may be in the dataStore in ANY order
I need to go thru the dataStore array (recursively if neccesary)
and output each child to the equivalent of a list box in the proper order.
The code I have does properly figure out the indent, just not the top to bottom order

HELP???

3

OK so one of the orderings is a “queue” - depth first

Off the top of my head in your case you could do something like
All written in the editor in the forum so there might be bugs :slight_smile:

dim queue() as string
dim processed as new dictionary

queue.append "" // the root
processed.value("") = true

while queue.ubound >= 0
        dim current as string = queue(0)
        queue.remove 0

        print current // or somehow "process this one"

        for i as integer = 0 to structurelist.ubound
           if parent = current and processed.HasKey(child)= false then

               queue.append child // although we might use a dictionary 
                                            // as we have to be careful not to add the same item
                                            // many times

                processed.value(child) = true

           end if
        next

end while
4

Thanks… I will see if I can adapt that… will let you know :smiley:

5

Ok… I came up with a way… inspired in part by what you posted :slight_smile:

this was the input (1st is Parent, 2nd is Child, 3rd it “Text”)

self.add( "" ,"A","A")
        self.add( "A","B","B")
        self.add( "A","G","G")
        self.add( "A","J","J")
        self.add( "B","C","C")
        self.add( "B","D","D")
        self.add( "D","E","E")
        self.add( "D","F","F")
        self.add( "G","H","H")
        self.add( "G","I","I")
updateDataStore()

 private func updateDataStore() {
        dataSTORE.removeAll()
        if treeNODES.count>0 {
            for i in(0...treeNODES.count-1) { treeNODES[i].level = -1 }
            addBranch("",0)
        }
    }
    private func addBranch(_ parent:String,_ lvl:Int) {
        var didAdd : Int = 0
        if treeNODES.count>0 {
            for i in(0...treeNODES.count-1) {
                if treeNODES[i].level<0 {
                    var newLevel : Int = -1
                    if treeNODES[i].parent == parent  { newLevel=lvl }
                    if treeNODES[i].child  == parent { newLevel=lvl+1 }
                    if newLevel>=0 {
                        treeNODES[i].level=newLevel
                        dataSTORE.append(treeNODES[i])
                        didAdd += 1
                        addBranch(treeNODES[i].child,newLevel+1)
                    }
                }
            }
            if didAdd>0 { addBranch("",0) }
        }
        theTABLE.reloadData()
    }
}

results were
tree