A Xojo issue or I'm not writing my code properly?

[anic297]

@MarkusWinter

What is easy to understand is that the sum of any two sides of a triangle must be larger than the third (just draw one long base and two short arms - the arms will never be able to meet to complete the triangle)…

Yes, that’s easy to understand and not part of my confusion (as is the sum of the angles being 180°).

The “only” area I don’t understand with triangles are the trigonometric function (cos, sin, tan, acts, atan and asin) because their results are meaningless to me (e.g. the cos of 45° is 0,707106781186548; well, what does that number mean to me? It’s an “abstract” number I can’t handle without using another function to convert it back to something meaningful).
And I’m not patient enough with abstract things, I know.

But, well, I’ve re-checked my formulas (for the nth time…). As you can see in my initial post, I was using sin for the hypotenuse; turns out I need cos…
And it’s actually what Alberto told me in his reply (which I overlooked ). Sorry.

Now, the hypotenuse is 576 (was 101 before), which is clearly better

Thank you all.

[MarkusWinter]

@anic297

But, well, I’ve re-checked my formulas (for the nth time…). As you can see in my initial post, I was using sin for the hypotenuse; turns out I need cos…

And that is why I asked what is what in your description.

Because sin(alpha) = cos( 90 - alpha ) = cos( beta )

So it makes a difference if you mean you have side a and alpha or side a and beta.

[anic297]

@MarkusWinter

And that is why I asked what is what in your description.

Yes, this was a flaw in my description, I recognise.

@MarkusWinter

Because sin(alpha) = cos( 90 - alpha ) = cos( beta )

Good to know; hope I’ll remember that (as it’s not a straight logic to me).
Thank you.

[MarkusWinter]

@anic297

e.g. the cos of 45° is 0,707106781186548; well, what does that number mean to me? It’s an “abstract” number

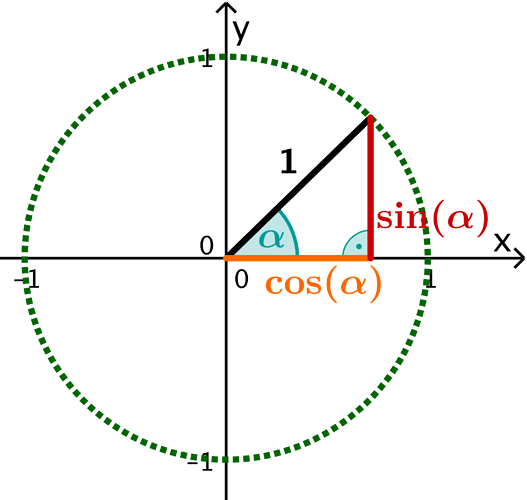
There are few things in Maths less “abstract” than sinus and cosinus.

Look at a “standard” circle (with a radius of 1 to make things easier):

That’s what sinus and cosinus are. Abstract? Absolutely not.

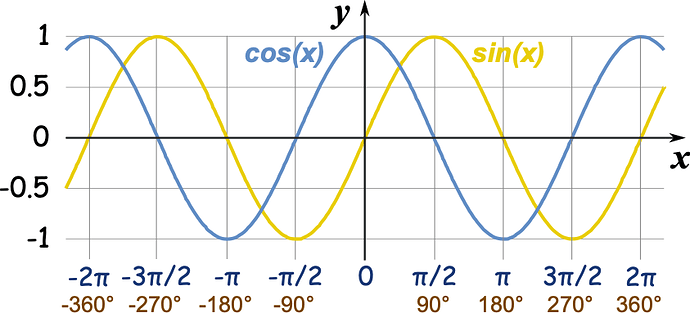
You can also see that sin(x) and cos(x) vary between -1 and 1

If the radius is twice as large, then sinus and cos are twice as large (you multiply with the radius)

sin(alpha) in a circle of radius 1 = 1 * sin(alpha)
sin(alpha) in a larger/smaller circle of radius r = r * sin(alpha)

@anic297

@MarkusWinter

Because sin(alpha) = cos( 90 - alpha ) = cos( beta )

Good to know; hope I’ll remember that (as it’s not a straight logic to me).

As you can see sin and cos are related by 90 degree.

You can easily see that if you plot sin and cos against the angle alpha or the arc length (remember that 360 degree = the circumference of the circle = 2 * radius * pi and as the radius is 1 it is ≈ 6.283185307…) as shown in this graph:

sinus and cosinus look the same, just moved by 90 degree = π / 2 ≈ 1.570796327

Now remember for graphs that if you add something to the FUNCTION you move the graph UP (eg the graph for x^2 + 1 is the x^2 graph moved up by 1), and if you subtract something you move it DOWN.

To move it LEFT and RIGHT you add/subtract something in the function argument, (x+1)^2 would move the parable graph to the LEFT, and (x-1)^2 would move the graph to the RIGHT.

If you make the FUNCTION negative then you mirror on the horizontal axis (eg x^2 vs -x^2), and if you make the variable negative you mirror on the vertical axis, eg (-x)^2 … which incidentally looks the same as x^2, so better compare (x-1)^2 with (-x-1)^2

Now on a circle whether you go 90 degree one way or 270 degree the other way, you still end up at the same spot.

So we could write

normal sinus curve: sin(alpha) =
cosinus curve moved to the RIGHT by 90: cos(alpha - 90) =
cosinus curve moved to the LEFT by 270: cos(alpha + 270) =
cosinus curve mirrored on vertical axis and moved to the RIGHT by 90: cos(90 - alpha) = cos( -alpha + 90) =
cosinus curve mirrored on vertical axis and moved to the LEFT by 270: cos(-270 - alpha) = cos( -alpha - 270) =
cosinus curve mirrored on horizontal axis and moved to the LEFT by 90: -cos(alpha + 90) = cos( -alpha + 90) =
cosinus curve mirrored on horizontal axis and moved to the RIGHT by 270: -cos(alpha - 270) = cos( -alpha - 270) =
or … etc etc

Boogles the mind but it all comes down to that in a circle you can go round and round and round - and the values just keep repeating … so the graph goes up and down and up and down and … until you go

[anon76569242]

EDIT: I want to add one comment to Markus’ thorough explanation: sine and cosine are just projections of a line of length = 1 on the other two directions.

@anic297

@MarkusWinter

Because sin(alpha) = cos( 90 - alpha ) = cos( beta )

Good to know; hope I’ll remember that (as it’s not a straight logic to me).
Thank you.

Now that Markus has explained the meaning of sine and cosine (and hopefully it is clear to you), you don’t need to remember that relationship because you can derive it yourself each time you need it. Take Markus’ circle and draw two lines, one at 30 º and the other one at 60 º (so, alpha and 90-alpha) and compare their sine and cosine values.

You could do the same with alpha and alpha + 90 º, also alpha and 180 - alpha, alpha and -alpha, … which all have relationships similar to the one Markus wrote.

Julen

[MarkusWinter]

And of course good old Pythagoras comes in here too:

a^2 + b^2 = c^2 (with c being the hypothenuse in a right triangle and a and b the arms)

sin(alpha) ^2 + cos(alpha) ^2 = 1

… good times …

[MarkusWinter]

Btw imagine the circle build from glass, and you mark a dot on its circumference in red.

Now rotate the circle at a constant speed.

Now look at that circle from the side - you’ll see the dot go up and down.

Now move the rotating circle at a constant speed forward, all the while looking at it edge on - you’ll see the dot going up and down but also going forward in space, and if you mark the positions that you see it results in the sinus wave form.

I’ll leave it to you to see what happens if you rotate or move the circle faster / slower … or make the circle bigger … as I said, there are few things in Maths less abstract than sinus

[anic297]

A lot of great explanations here, thank you!
Yes, it’s obviously less abstract with visualising a circle.

What I didn’t see correctly until now is why cos and sin are always between -1 and 1 and what that number represents. 1 and -1 are the “100%” of the possible value (as the circle with a radius of 1 shows).

If the radius is 2, it’s not the sin or cos that doubles, it’s their result.
Sin and cos are “constant for a given angle of a circle of radius 1” (as would imply the result of these functions), but the reasoning behind this, I could only understand it with a circle to visualise, I think.

@anon76569242

Now that Markus has explained the meaning of sine and cosine (and hopefully it is clear to you), you don’t need to remember that relationship because you can derive it yourself each time you need it.

Clear, yes. If I take the time to visualise the circle…
Granted, trying to understand the relationship between, say, 80 and its cos value (0,17364817766693) is hard unless you “think visually” (which is one of my issues, always has been).

@MarkusWinter

Btw imagine the circle build from glass, and you mark a dot on its circumference in red.

Remembering my electricity courses I’ve had…
Yes, this is perfectly clear. For whatever reason, the cos and sin function are harder for me to assimilate (almost impossible without the image of a circle).

[MarkusWinter]

@anic297

If the radius is 2, it’s not the sin or cos that doubles, it’s their result.
Sin and cos are “constant for a given angle of a circle of radius 1” (as would imply the result of these functions), but the reasoning behind this, I could only understand it with a circle to visualise, I think.

They are constant for a certain angle for any circle of any size.

Because what they represent is the ratio between the “arm” and the hypothenuse for a given angle, e.g. (if you label the triangle in the circle like the ABC triangle further up)

sin(alpha) = a / c

cos(alpha) = b / c

And for a given angle that ratio does not change no matter how big the circle is (because a, b, c all grow or shrink by the same factor), so

sin(alpha) = a / c = 2 a / 2 c = 3.4 a / 3.4 c …

There are several mathematical methods to calculate the values, but don’t be disturbed when you discover that most are approximations (and the Ancients probably just made a very big circle, measured them and created lookup tables). After all, pi is involved and there 3.14159 is plenty precise for most calculations.